Метод круглоцилиндрических поверхностей скольжения
Реальные грунты, как правило, обладают не только сцеплением, но и трением. В связи с этим проблема устойчивости откосов становится значительно сложнее, чем в рассмотренных случаях. Поэтому на практике для решения задач в строгой постановке, большое распространение получил метод круглоцилиндрических поверхностей скольжения.
Теория предельного равновесия грунтов, развитая В.В. Соколовским, позволяет решать задачи двух типов:
- задан угол наклона плоского откоса, определяется интенсивность
внешней нагрузки на верхней горизонтальной поверхности грунта, офаниченного откосом массива; - задана интенсивность нагрузки на верхней горизонтальной поверхности
грунта, офаниченного откосом массива, определяется форма равноустойчивого
откоса, находящегося в предельном напряженном состоянии.
Задача первого типа, при однородных грунтах и плоском откосе (рис. 9.6) решена В.В. Соколовским в безразмерных величинах q (табл. 9.1).
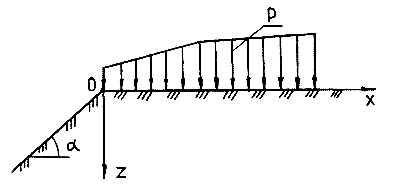
Рис. 9.6. Схема к расчету устойчивости плоского откоса по теории предельного равновесия
Таблица 9.1. Значения безразмерного коэффициента q
| X | При φ, град. | |||||||||||
| 10 | 20 | 30 | 40 | |||||||||
| При α, град. | ||||||||||||
| 0 | 10 | 0 | 10 | 20 | 10 | 20 | 30 | 10 | 20 | 30 | 40 | |
| 0 | 8,3 | 7,5 | 14,8 | 12,7 | 10,9 | 24,3 | 19,6 | 15,7 | 55,9 | 41,4 | 30,6 | 22,5 |
| 1 | 9,6 | 8,2 | 20,6 | 16,6 | 13,1 | 39,8 | 28,8 | 20,3 | 126,0 | 81,1 | 50,9 | 31,0 |
| 2 | 10,8 | 8,9 | 25,4 | 19,9 | 15,0 | 52,9 | 36,7 | 24,2 | 186,0 | 115,0 | 68,4 | 38,1 |
| 3 | 11,8 | 9,6 | 29,8 | 23,0 | 16,7 | 65,1 | 44,1 | 27,8 | 243,0 | 148,0 | 84,9 | 44,4 |
| 4 | 12,8 | 10,2 | 34,0 | 25,8 | 18,3 | 76,8 | 51,2 | 31,1 | 299,0 | 179,0 | 101,0 | 50,4 |
| 5 | 13,7 | 10,8 | 38,0 | 28,7 | 19,9 | 88,3 | 58,1 | 34,3 | 354,0 | 211,0 | 117,0 | 56,2 |
| 6 | 14,5 | 11,3 | 41,8 | 31,4 | 21,4 | 99,6 | 65,0 | 37,4 | 409,0 | 241,0 | 132,0 | 61,7 |
Исходными уравнениями для решения этой задачи являются:
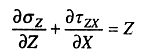 (9.8)
(9.8)
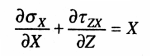 (9.9.)
(9.9.)
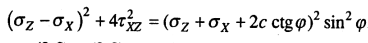 (9.10)
(9.10)
Выражения (9.8) и (9.9), как было выше сказано, представляют дифференциальные уравнения равновесия, а (9.10) — условие предельного равновесия.
Предельная нагрузка на верхней горизонтальной поверхности откоса, зная q , определяется из выражения
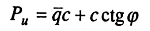 (9.11)
(9.11)
где q — безразмерный коэффициент, зависящий от углов внутреннего
трения φ, угла α и расстояния х от края откоса до
рассматриваемой точки (см. табл. 9.1).
Задача второго типа для
случаев, когда на верхней горизонтальной поверхности откоса распределена
равномерная нагрузка (по В.В. Соколовскому):
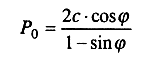 (9.12)
(9.12)
и надо найти равноустойчивый откос.
Для случаев, когда с≠0 и φ≠0, с помощью численного интегрирования дифференциальных уравнений получены очертания равноустойчивых откосов в безразмерных коэффициентах, которые представлены на рис. 9.7.
Согласно рис. 9.7 для нахождения действующего очертания равноустойчивого откоса определяют Х и Z:
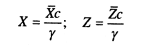 (9.13)
(9.13)
и строят равноустойчивый откос, начиная с его верхней кромки.
При угле внутреннего трения φ = 0 устойчивость откоса определяется силами сцепления:
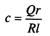 (9.14)
(9.14)
где с — удельная сила сцепления, обеспечивающая устойчивость откоса; Q — масса призмы обрушения (рис. 9.8,а) равная Q= γ·h; h — высота откоса; γ — удельный вес оползающего грунта; r — плечо сиилы относительно центра О; l — длина дуги поверхности скольжения.
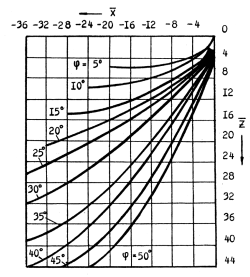
Рис.9.7. Графики для построения равноустойчивых контуров откосов в безразмерных координатов
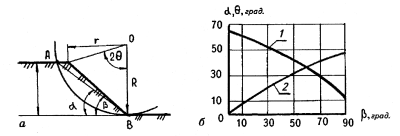
Рис. 9.8. Схемы к расчету устойчивости откоса:
1- зависимость ∟α от
β; 2 - зависимость ∟θ от ∟β; γ - удельный вес оползающего грунта; r — плечо силы
относительного центра О; R— радиус поверхности скольжения; l -
длина дуги поверхности скольжения.
Откос находится в устойчивом состоянии, если величина фактической силы сцепления с будет больше или равна критической сcv или максимальной удельной силе сцепления:
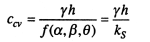 (9.15)
(9.15)
Вероятная поверхность скольжения пройдет через подошву откоса по такой дуге окружности, для которой требуется ccv. При известном значении угла β значения углов α и θ и, следовательно, положение центра О определяют по графику Феллениуса (см. рис. 9.8,6).
Большое распространение на практике получил метод круглоцилиндрических поверхностей скольжения, сущность этого метода заключается в отыскании круглоцилиндрической поверхности скольжения с центром в некоторой точке О, проходящей через подошву откоса, для которой коэффициент устойчивости будет минимальным (рис. 9.9).
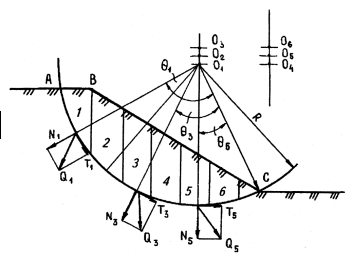
Рис. 9. 9. Схема к расчету устойчивости откоса методом круглоцилиндрической поверхности скольжения
Расчет ведется для отсека, для чего оползающий клин ABC разбивается на n вертикальных отсеков. Делается предположение, что нормальные и касательные напряжения, действующие по поверхности скольжения, в пределах каждого из отсеков оползающего клина определяются весом данного отсека Qi, и равны соответственно:
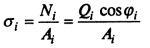 (9.16)
(9.16)
 (9.17)
(9.17)
Здесь
Ai
— площадь поверхности скольжения в
пределах i-го вертикального отсека, Ai=
1li; li
— длина дуги скольжения в плоскости
чертежа (см. рис. 9.9).
Препятствующее оползанию откоса сопротивление сдвигу по рассматриваемой поверхности в предельном состоянии
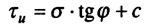 (9.18)
(9.18)
Из (9.16)—(9.18) следует выражение для силы сопротивления сдвигу в пределах i-го отсека:
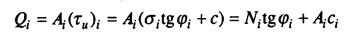 (9.19)
(9.19)
Устойчивость откоса можно оценить отношением моментов удерживающих Ms,l и сдвигающих Ms,a сил. Соответственно коэффициент запаса устойчивости определим по формуле
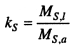 (9.20)
(9.20)
Момент удерживающих сил относительно О представляет собой момент сил Qi:
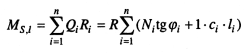 (9.21)
(9.21)
Момент сдвигающих сил относительно точки О
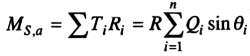 (9.22)
(9.22)
Тогда формулу (9.19) можно записать в следующем виде:
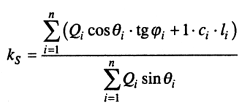 (9.23)
(9.23)
При наличии подземных вод учитывают фильтрационное давление, которое будет уменьшать устойчивость откоса. Фильтрационное давление определяют как нормальную составляющую:
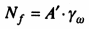 (9.24)
(9.24)
для i-й призмы или отсека
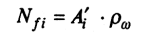
где А'— площадь, занятая фильтрационным потоком в оползающей призме грунта, равная А' = А'1 + А'2 + А'3 (рис. 9.10); γω — удельный вес воды.
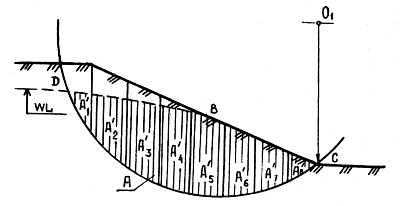
Рис. 9.10. Схема к определению площади, занятой фильтрационным потоком
Фильтрационное давление влияет только на нормальную составляющую формулы (9.23).
Устойчивость откоса согласно изложенной расчетной методике обеспечена, если ks>1. При проектировании сооружений коэффициент устойчивости назначают обычно в пределах 1,2—1,3.
Для решения практических задач установлен следующий порядок расчета. Из некоторого произвольного центра О1 радиусом R через точку С проводят поверхность скольжения (см. рис. 9.9). Участок откоса, ограниченный дугой АС и ломаной линией откоса ABC, разбивают на ряд призм равной ширины, массу которых подсчитывают как площади соответствующих фигур, умноженных на удельный вес грунта. При наличии в откосе грунтов с различным удельным весом строят фиктивный профиль с удельным весом, приведенным к одному из имеющихся.
Далее по формуле (9.23) определяют коэффициент устойчивости. После того повторяют построения и расчеты при цилиндрических поверхностях скольжения, проведенных из новых центров О2, О3 и т.д. до тех пор, пока не будет найдено минимальное значение ks на первой вертикали. Аналогично проводят расчет, определяя минимальное значение коэффициента устойчивости для второй вертикали, строя круглоцилиндрические поверхности, проведенные из центров O4, O5, O6. Затем такие же расчеты повторяют для третьей, четвертой и т.д. вертикалей, пока не будет определен самый минимальный коэффициент устойчивости. Поверхность скольжения, имеющая наименьшую величину ks, будет наиболее вероятной поверхностью скольжения грунтов склона.



