При проектировании оснований сооружений одним из основных условий является ограничение перемещений предельными их значениями, т.е. производится расчет по второй группе предельных состояний.
Совместная деформация основания и сооружения может характеризоваться:
- абсолютной (конечной) осадкой отдельного фундамента S;
- средней осадкой основания сооружения;
- относительной неравномерностью осадок фундаментов ∆S/L;
- креном фундамента или сооружения в целом i;
- горизонтальным перемещением фундамента или сооружения в целом и.
Расчет оснований гидротехнических сооружений по второй группе предельных состояний (по деформациям) заключается в выполнении условий:
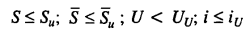(7.3)
где Su; Su ; UU; iU — соответственно предельные абсолютные и средние осадки, горизонтальные перемещения и крены, при которых гарантируются нормальные условия эксплуатации и обеспечивается требуемая долговечность сооружения (принимаются по СНиП 2.02.01—83*).
Левая часть неравенства S ≤ Su характеризует деформируемость грунтов основания. Она учитывает общие инженерно-геологические условия строительной площадки, особенности напластования и свойств грунтов основания.
Правая часть неравенства S≤Su учитывает особенности проектируемых зданий и сооружений, условия их эксплуатации и напряженные состояния надземных частей зданий и сооружений. Чем ближе S и Su, тем экономичнее будут запроектированы основание и фундамент.
Для определения осадок основания выбирается расчетная схема с учетом показателей механических свойств, характера их напластования в основании и особенностей сооружения.
Наиболее употребимыми при проектировании являются следующие методы расчета осадки:
- определение осадки слоя грунта при сплошной неравномерной нагрузке (основная задача);
- определение осадки неоднородного (слоистого) грунта основания (линейно-деформируемого полупространства) — метод послойного суммирования;
- определение осадок линейно-деформируемого слоя конечной толщины;
- расчет осадки во времени;
- определение неравномерности осадок и крена фундамента.
Основная задача. При действии сплошной нагрузки, распространенной на значительные расстояния в стороны, слой грунта испытывает только сжатие без возможности бокового расширения, т.е. аналогично компрессионному сжатию (рис. 7.10,а).
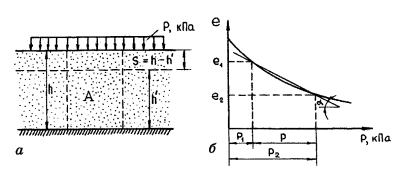
Рис. 7.10. Схема испытания грунта при сплошной нагрузке: а — схема нагрузки; б — компрессионная кривая
В этом случае будем иметь строго одномерную задачу компрессионного уплотнения грунтов и для определения полной стабилизированной осадки слоя грунта воспользуемся результатами компрессионных испытаний (см. рис. 7.10,б).
Осадка грунта происходит из-за изменения объема за счет уменьшения пористости при увеличении внешнего давления, а объем твердых частиц, как было ранее сказано, при этом остается неизменным.
Выделим в рассматриваемом слое (см. рис. 7.10,а) на всю его высоту
цилиндр площадью поперечного сечения А, принимая во внимание, что
объем
твердых частиц Vs в единице объема грунта равен
m = 1 / 1 + e, так как m+n=1.
Приравняем Vs выделенного цилиндра до приложения нагрузки к объему после полного компрессионного уплотнения под нагрузкой.
Тогда
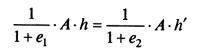(7.4)
где е1 — начальный коэффициент пористости,
соответствующий условиям естественного залегания; е2 — то
же, после действия внешней нагрузки; h — высота слоя грунта;
h'
— конечная (стабилизированная после уплотнения) высота слоя грунта.
Сократив обе части уравнения (7.4), получим
формула (7.5)
Согласно рис. 7.10,а осадка S равна разности высот грунта до уплотнения нагрузкой и после, тогда получим
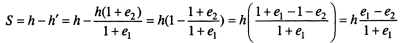
Таким образом, осадка слоя грунта при сплошной нагрузке определяется по формуле
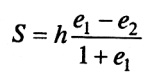(7.6)
Учитывая, что изменение коэффициента пористости прямо пропорционально изменению давления, т.е. е1 - е2 = m0(Р2— Р1) = m0P, получим
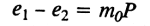(7.7).
Подставив (7.7) в (7.6) получим
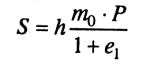(7.8)
где m0 / 1+e1 = mv есть коэффициент относительной сжимаемости грунта.
Подставляя в (7.8), получим наиболее простой вид формулы для осадки слоя грунта при сплошной нагрузке
S=mv·h·P (7.9)
Так как
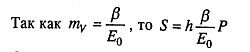(7.10)
где β — коэффициент, который зависит от коэффициента относительной поперечной деформации грунта (аналогично коэффициенту Пуассона): для песков β = 0,8; супесей β = 0,7; суглинков β = 0,5; глин β = 0,4.
Эта формула (7.10) справедлива для любых грунтов в пределах линейной зависимости между напряжениями и общими деформациями.
