Построение круга Мора
Круг Мора (рис. 8.2) вычерчивается в прямоугольной системе координат. Полагается, что σ1≥σ2
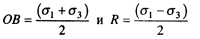
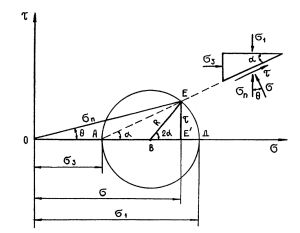
Рис. 8.2. Графическое представление напряженного состояния грунта (круг Мора)
Построение круга Мора производится в следующей последовательности. От начала координат откладываем значения σ1 и σ3. Из точки В проводят окружность радиусомт R. Любая точка E на окружности характеризует напряженное состояние грунта в плоскости, проходящей через рассматриваемую точку. Угол наклона α линии ЕА — это угол наклона рассматриваемой площадки к главной. Центральный угол наклона отрезка EB равен 2α. Нормальные напряжения по этой площадке а представляются по горизонтальной оси отрезком ОЕ', касательные τ — перпендикулярным отрезком ЕЕ'.
Значения σ и τ могут быть определены через σ1 и σ3 по формулам (8.1) и (8.2).
Максимальные и минимальные касательные напряжения соответствуют sin 2α = 1 и sin 2α = -1, т.е. углам 2α=π/2 или 3π/2 (α=45° или 135°).
Полное результирующее напряжение на рассматриваемой площадке
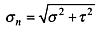
Угол отклонения σn от нормали к площадке
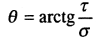(8.4)
Значение угла θ при изменении угла α от 0 до 90° сначала возрастает от нуля до некоторого θmax, а затем убывает до нуля.
Угол θ максимален, когда линия ОE станет касательной к кругу напряжений. Из треугольника ОBЕ:
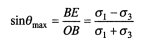(8.5)
Максимальное отклонение полного (результирующего) напряжения на угол θmax нормали к площадке имеет место при:
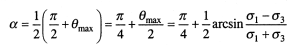(8.6)
Следовательно, отклонения площадки скольжения от направления наибольшего главного напряжения σ1
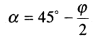(8.7)
Таким образом, в предельном состоянии в каждой точке грунта имеются две сопряженные площадки скольжения, наклоненные под углом 45°- φ/2 к линии действия максимального и 45° + φ/2 — минимального главного напряжения (рис. 8.3).
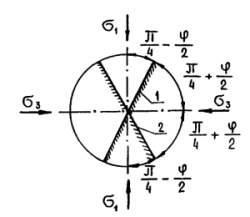
Рис. 8.3. Ориентация площадок скольжения относительно главных напряжений: 1, 2 — площадки скольжения
Для сыпучих грунтов во всех случаях θmax не может быть больше угла внутреннего трения φ. А разрушение сыпучих грунтов наступает, когда угол отклонения полного(результирующего) напряжения равен углу внутреннего трения:
θmax = φ (8.8)
Выражение (8.8) является условием прочности грунта. Тогда уравнение предельного равновесия можно записать в следующем виде:
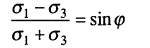(8.9)
Выражение (8.9) известно в механике грунтов как условие прочности (предельного равновесия) для песчаных (сыпучих) грунтов. После несложных тригонометрических преобразований это выражение можно записать в следующем виде:
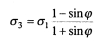(8.10)
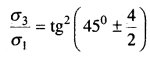(8.11)
Это выражение часто используют в теории давления грунтов на ограждения (глава 10). Для связных грунтов также можно записать условие предельного равновесия, предварительно построив круги Мора (рис. 8.4) по результатам испытания в стабилометре (см. рис. 5.7).
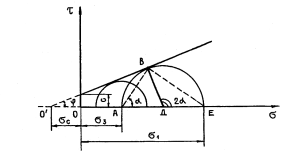
Рис. 8.4. Круги Мора, построенные по результатам испытания образцов грунта на сжатие в стабилометре
Радиус круга
ВД = (σ1-σ3)/2 (8.12)
а отрезок О'Д можно найти из выражения
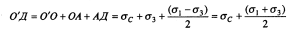(8.13)
Отрезок О'О, отсекаемый наклонной линией на оси абсцисс (см. рис. 8.4), называют давлением связности, которое можно представить в виде
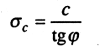(8.14)
Давление связности (8.14) можно условно считать начальным давлением связного грунта, которое необходимо преодолеть при испытании на сдвиг. Зная ВД (8.12) и О'Д (8.13), а также используя (8.14), найдем
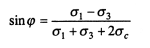(8.15)
Выражение (8.15), связывающее главные напряжения в момент разрушения образца с углом внутреннего трения, принято называть уравнением предельного равновесия для связных грунтов.
Уравнение (8.15) в некоторых случаях удобно использовать не в главных напряжениях, а в компонентах, записанных относительно координатных осей. Из сопротивления материалов известно, что:
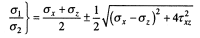(8.16)
Тогда, рассматривая совместно уравнения (8.15) и (8.16), можно записать уравнение предельного равновесия в следующем виде:
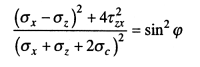(8.17)
Аналогичным образом можно выразить и уравнение (8.9).
